“When you can measure what you are speaking about, and express it in numbers, you know something about it” - Lord Kelvin

In packet-switched networks, buffers serve an essential function by temporarily storing packets, which helps smooth out bursts of incoming traffic and manage mismatches between the rates of incoming and outgoing links. However, since buffers have limited capacity, running out of buffer space leads to packet loss.

Traditional methods, like Tail Drop, only discard packets once the buffer is full. This approach can cause synchronized reactions across multiple data flows—known as global synchronization—which ultimately leads to inefficient network utilization and decreased throughput.

Active Queue Management (AQM) techniques tackle these problems by proactively controlling queue lengths. By detecting congestion early and dropping or marking packets before severe congestion occurs, AQM significantly improves network stability and resource utilization. While there are many possible queuing disciplines for packet scheduling, two key considerations must be assessed when selecting a discipline: its ability to ensure bounded delay and the efficiency of its implementation.

Packet Buffer Memory Structure

A packet buffer is divided into three distinct memory regions: Cell-data memory, Cell-pointer memory, and Packet Descriptor (PD) memory.

Cell-data memory serves as the primary storage area for the bytes of packet payloads. To optimize memory usage and prevent fragmentation, the payload data is segmented into fixed-sized blocks known as cells, each identified by a unique index. Depending on the length of the packet, the payload may occupy one or more of these cells.

The cell-pointer memory manages the links between individual cells. Each cell pointer is a small metadata structure that indicates the location of a cell and points to the next cell in a packet’s payload chain. When a packet enters the switch, a sequence of free cell pointers is allocated from a global linked list known as the free cell list. This free list is organized as a singly linked chain, which allows for constant-time (O(1)) allocation and deallocation of cells.

To allocate space for a new packet, the initial pointer of the packet is assigned to the current head of the free list, and then the head is moved to the next pointer in the list. This method eliminates the need for costly pointer writes for each cell. Similarly, once a packet has been transmitted and is no longer needed, its associated cell pointers can be returned efficiently by appending them back to the end of the global free list, again with minimal pointer updates.

Each packet entering the buffer is represented by a compact metadata structure known as a Packet Descriptor (PD). The PD contains essential information, such as the packet length and pointers that identify the beginning of the packet’s cell-pointer chain. Within the switch, queues, such as Virtual Output Queues (VOQs), are organized as linked lists of these PDs. The switch’s scheduler and traffic management logic interact directly with the PDs, rather than with the payload data.

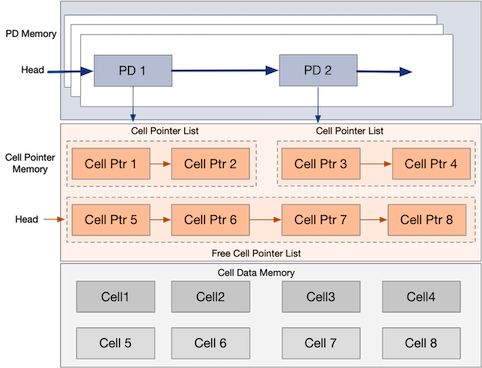
During normal operation, when a packet is ready for transmission, the scheduler removes the corresponding Packet Descriptor (PD) from its queue. The transmission pipeline then reads the packet’s cell pointers in order, using them to access and transmit the payload data from the cell-data memory. This retrieval process efficiently overlaps access to the PD memory, pointer memory, and cell-data memory.

Non-Preemptive Buffer Management

Non-preemptive buffer management (BM) refers to a group of schemes that only make admit or deny decisions upon the arrival of packets and do not evict packets that are already in the buffer. In practice, this is implemented by using threshold logic on the admission path: a queue can accept bytes as long as its instantaneous occupancy is below a certain threshold. However, once this threshold is crossed, any new arriving packets must be dropped or marked. Previously admitted packets are allowed to drain naturally at the egress share. This principle of “allocate-on-enqueue, return-on-dequeue” is appealing because it is straightforward and cost-effective to implement in the traffic manager datapath.

The dominant non-preemptive scheme used in merchant switch ASICs is known as Dynamic Threshold (DT). DT calculates a time-varying, per-queue threshold $T(t)$ that is proportional to the currently available shared buffer.

Here, $B$ represents the total shared buffer, $q_i(t)$ represents queue occupancies, and $\alpha$ is a gain factor (often a power of two, allowing the hardware to implement the multiplication as a shift). Intuitively, DT is generous when the switch is empty and tightens limits as the buffer fills, balancing efficiency and fairness without requiring per-queue reservations.

However, the design has two fundamental drawbacks, both of which stem from the nature of non-preemption. First, it lacks agility. Since previously accepted packets cannot be evicted, the only way to reduce an over-allocated queue is to wait for it to drain at its egress rate. During arrival spikes (such as incast) or when competing queues receive most of the scheduler’s share (either through strict or weighted priority), thresholds can decrease faster than these long-standing queues can be drained. This leads to the well-documented transient anomaly: newcomers may be dropped before achieving fairness while incumbents remain over-allocated, particularly when high-priority classes are starved by slowly draining low-priority queues.

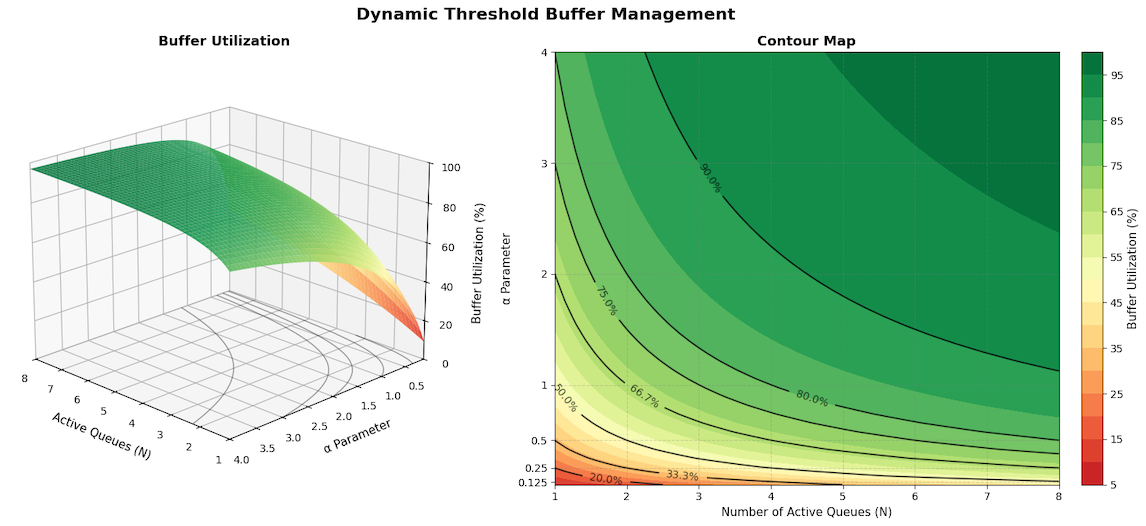
Secondly, there is a problem of inefficiency. Because non-preemptive BMs cannot quickly create space for newly active queues, they must proactively reserve free headroom to absorb transients—headroom that remains idle at the moment of a drop. Under realistic settings (e.g., $\alpha=0.5$), the 99th-percentile buffer utilization at the moment of a drop is only around 66%, which is a significant drawback given the scarcity of on-chip SRAM and the need for sufficient occupancy to handle both low-latency burst absorption and high throughput. Adjusting $\alpha$ reveals this trade-off rather than eliminating it: smaller values of $\alpha$ waste buffer space (resulting in more headroom and fewer drops), while larger values make DT more susceptible to anomalous behavior during bursts, as incumbents hold onto larger allocations that they cannot shed quickly.

Using the formula, we can get the Utilization $U(N,\alpha)$ and free head room $H(N,\alpha)$.

For $N=4$, and $\alpha=0.5$, Utilization (U) = 66.7% and free buffer space (H) 33.3%. Below is a plot showing the relation between the Queues, $\alpha$ and Buffer utilization.

Classic AQM Schemes

We examined the buffer memory structure and management. Now, we will shift our focus to Active Queue Management (AQM) schemes. AQM represents the router’s proactive approach to stabilizing the feedback loop between finite buffers and various end-host rate controllers. Instead of waiting for buffers to fill and then reacting with a tail-drop, AQM actively regulates admission pressure to ensure that queues remain short enough to limit delay while still being flexible enough to accommodate bursts of traffic. This process helps reduce unnecessary packet loss, prevents issues like “lock-out” caused by aggressive senders, avoids herd backoff (also known as global synchronization), and maintains efficient link utilization, even when many flows and service classes are competing for bandwidth. In essence, AQM determines when and how much congestion signal to generate, which allows scheduling to function on healthy queues. This capability is crucial regardless of whether the upstream controllers operate based on window size, rate, or application-driven methods.

RED and WRED

Random Early Detection (RED) is a foundational AQM algorithm. RED monitors the average queue length and, when congestion is building, begins dropping a probabilistic fraction of packets before the queue is full. As the average queue length grows from a minimum threshold to a maximum threshold, the drop probability increases from 0 to a configured maximum (linearly by default). By dropping (or marking) a few packets early, RED prompts some senders to slow down, thus avoiding a large burst of tail drops later. This reduces the likelihood of synchronized packet loss across flows and helps maintain lower average queue lengths.

Weighted RED (WRED) extends RED by supporting multiple traffic classes or priorities with different drop behaviors. Essentially, WRED is “RED with priorities” – it applies the RED algorithm on a per-class basis, allowing packets with lower priority (or DSCP markings) to face a higher drop probability earlier than high-priority packets. This way, WRED can preferentially protect critical traffic while still avoiding tail-drop for each class. In practice, this can be separate queues for classes with independent RED. WRED reduces the chances of tail drop by selectively dropping packets when the output interface begins to show signs of congestion. If congestion worsens beyond the RED range (i.e., the queue continues to fill), normal tail drop applies to any further packets.

Explicit Congestion Notification (ECN) Integration

ECN is an essential enhancement to Active Queue Management (AQM). Instead of dropping packets to signal congestion, the Random Early Detection (RED) or Weighted Random Early Detection (WRED) algorithms can mark packets with an ECN flag when certain thresholds are exceeded. This marking prompts the endpoints to react as they would to packet loss, but without actually losing data.

Typically, ECN is implemented as an extension of WRED. When the average queue length surpasses a specified threshold, the router or switch marks the ECN bits in the packet instead of dropping it. This approach enables early detection of congestion while preventing data loss.

Switches and routers usually enable ECN marking on queues using a RED-like AQM algorithm, which is often configured with two thresholds: a minimum threshold, where marking begins, and a higher maximum threshold, where the likelihood of marking or dropping packets reaches 100%. For instance, a switch might start marking packets with ECN when a queue exceeds 150 KB and may ramp up to marking or dropping all packets once the queue occupancy reaches 3 MB.

The primary advantage of ECN is that it enables congestion notification without causing packet loss.

How is the “Average Queue” computed?

WRED uses an exponentially weighted moving average (EWMA) of the instantaneous queue length to smooth bursts and react to persistent congestion. The critical factors which significantly impacts EWMA performance are:

• Weight ($w$)
• Nature of Network Traffic
• Samping Interval Duration

If $Q_{\text{avg(k)}}$ is the filtered (average) queue length, and $Q_{\text{sample(k)}}$ is the instantaneous queue occupancy when we update, the recurrence is:

Equivalently,

with $0\le w\le 1$. In hardware, $w$ is chosen as a negative power of two, $w=2^{-n}$ , so the multiply becomes a shift which is pretty easy to implement in hardware.

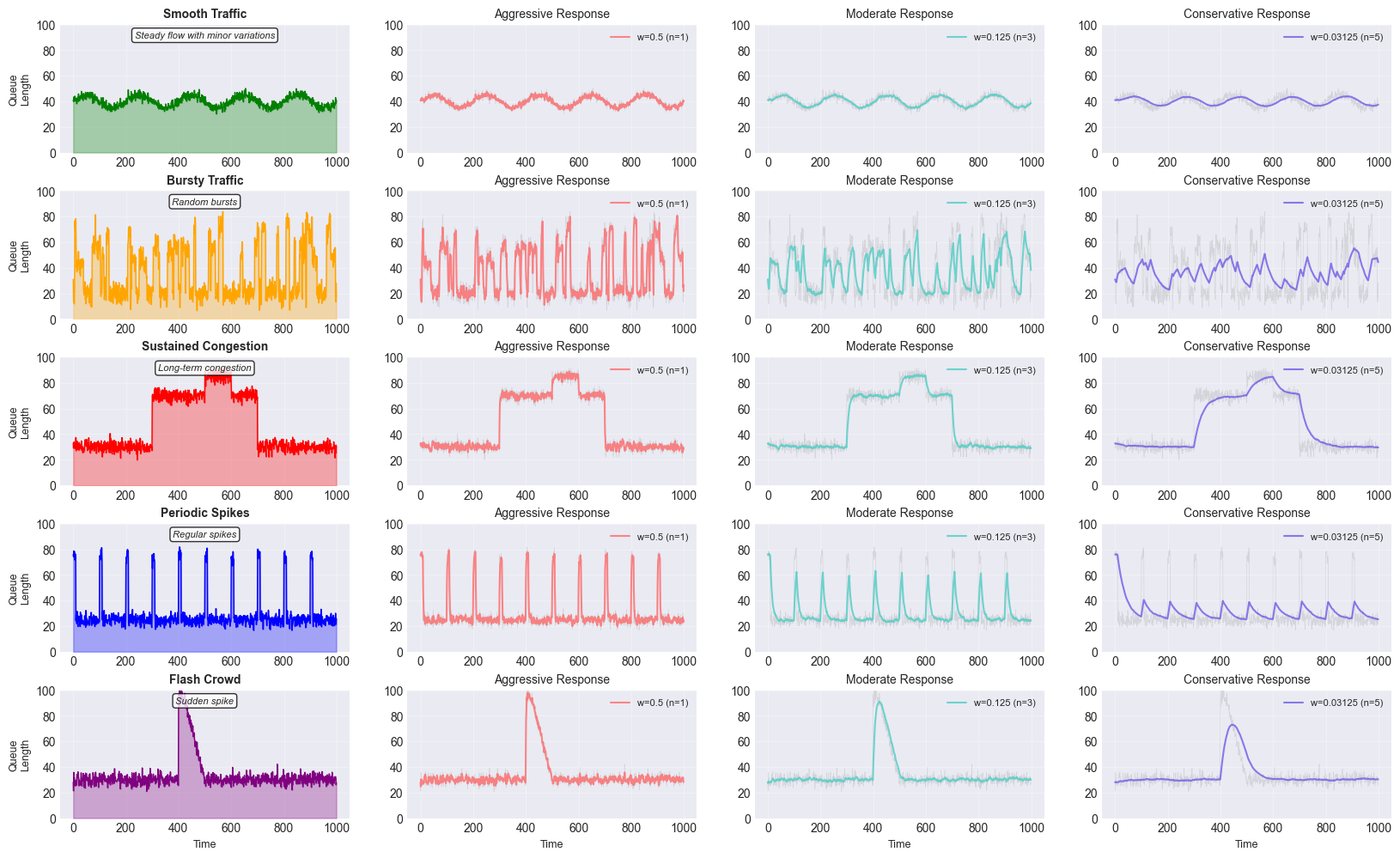
Here, $w$ determines the responsiveness and stability of the average:

• Large $w \to$ faster reaction, less smoothing (more sensitive to short spikes).
• Small $w \to$ slower reaction, more smoothing (less sensitive to short spikes).

Below is a plot which shows how well different values of weight from higher to lower captures the original signal.

Averages can lie: Why the Mean Can Be… Mean

As you saw in earlier section that averages compress shape. The below example shows many datasets with the same mean and variance but wildly different patterns. Queues do this too.

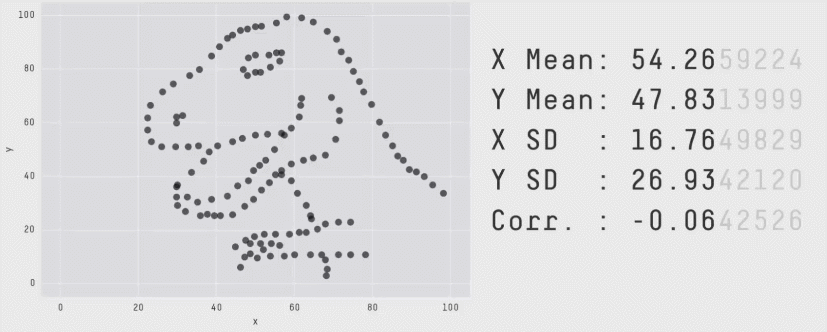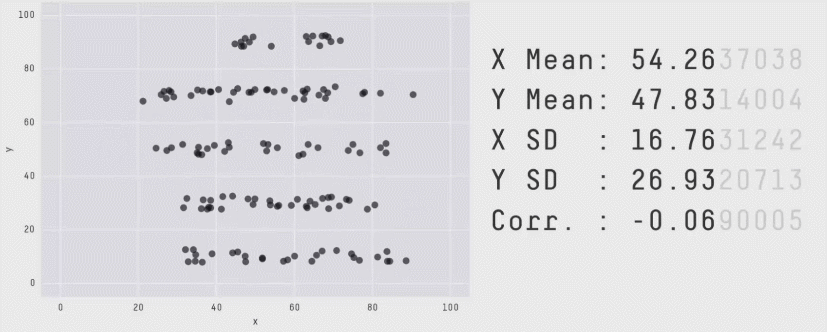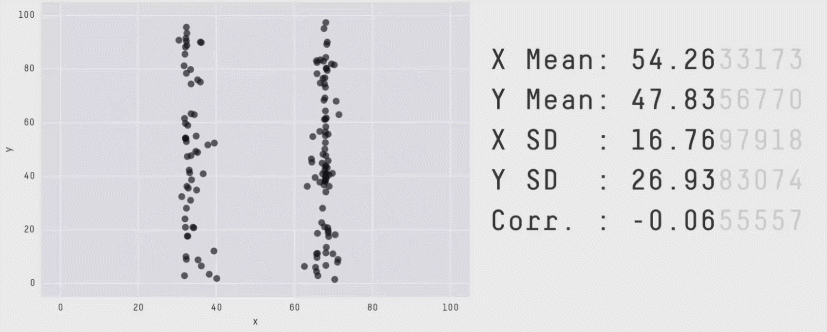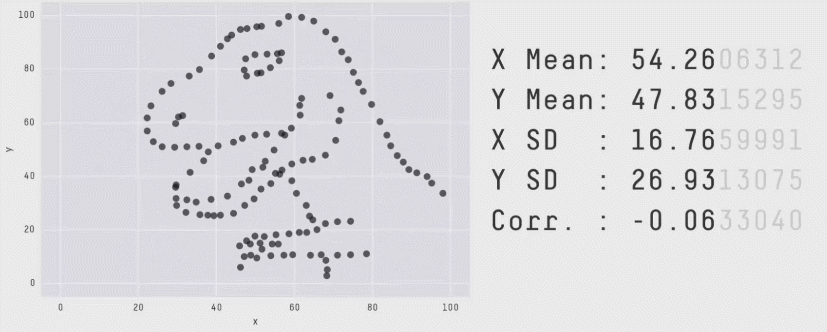
Ref: Same State different Graph

• Same mean, different pain. A queue that sits near 20 KB all the time behaves very differently from one that idles at 0 and spikes to 100 KB. The average is 20 KB in both, but only the spiky one blows past ECN thresholds, drives P99 latency, and triggers drops/trim.

• EWMA can hide spikes. A slow EWMA smooths bursty queues into a “nice” average; packets still saw the spike. Tune half-life from time goals, but validate on instant occupancy.

Signal Processing Foundations of EWMA

EWMA comes from signal processing theory, where it’s used to filter noisy signals. You’ll find the same mathematics in financial analysis, control systems, and anywhere else that needs to smooth time-series data.

Impulse Response

The impulse response answers a simple question: “If a single spike appears in otherwise steady data, how long does EWMA remember it?”

Consider a temperature sensor that has been reading a steady 20C for hours. At time t=0, there’s a brief spike to 30C—just one reading—then immediately back to 20C. The impulse response tells us how that single 10-degree spike affects all future EWMA values.

Mathematically, for a unit impulse at t=0 (value of 1 at t=0, zero everywhere else), the EWMA response at time k is: \(h_k = w(1-w)^k\) This reveals a crucial insight: the influence of any single observation decays exponentially. Let’s see this with $w=0.2$:

• At time 0: $0.2 \times (0.8)^0 = 0.2$
• At time 1: $0.2 \times (0.8)^1 = 0.16$
• At time 2: $0.2 \times (0.8)^2 = 0.128$
• At time 3: $0.2 \times (0.8)^3 = 0.1024$

The pattern is clear: each time step multiplies the remaining influence by (1-w). This creates a fundamental tradeoff:

• Larger w: Strong initial response (captures more of the spike) but forgets quickly (influence drops fast)
• Smaller w: Gentle initial response (captures less of the spike) but remembers longer (influence persists)

This is why choosing $w$ is about deciding what matters more: responsiveness to changes or stability against noise.

Memory Characteristics

While impulse response shows how quickly a spike fades, memory characteristics answer a different question: “How many past observations actually influence the current EWMA value?”

The key metric here is the effective memory length—roughly how many recent observations meaningfully contribute to the current average:

For example, with , the effective memory is observations and with , the effective memory is observations. This means the EWMA behaves roughly as if it’s averaging the last 19 data points with $w=0.1$. With $w=0.8$, effective memory $\approx$ 1.5 datapoints, i.e. EWMA barely looks beyound the last couple of values.

This reveals the fundamental memory tradeoff:

Short memory (w close to 1): The filter tracks the input signal with minimal smoothing. You get a rapid response to changes, but also inherit most of the noise. Think of it as having tunnel vision on the most recent data.

Long memory (w close to 0): The filter considers many past observations, heavily smoothing the output. You get stable, noise-free estimates but sluggish response to actual changes. It’s like having a wide-angle view that includes lots of history.

The figure below illustrates this memory effect in action, where a single spike is remembered by the EWMA process for different weights.

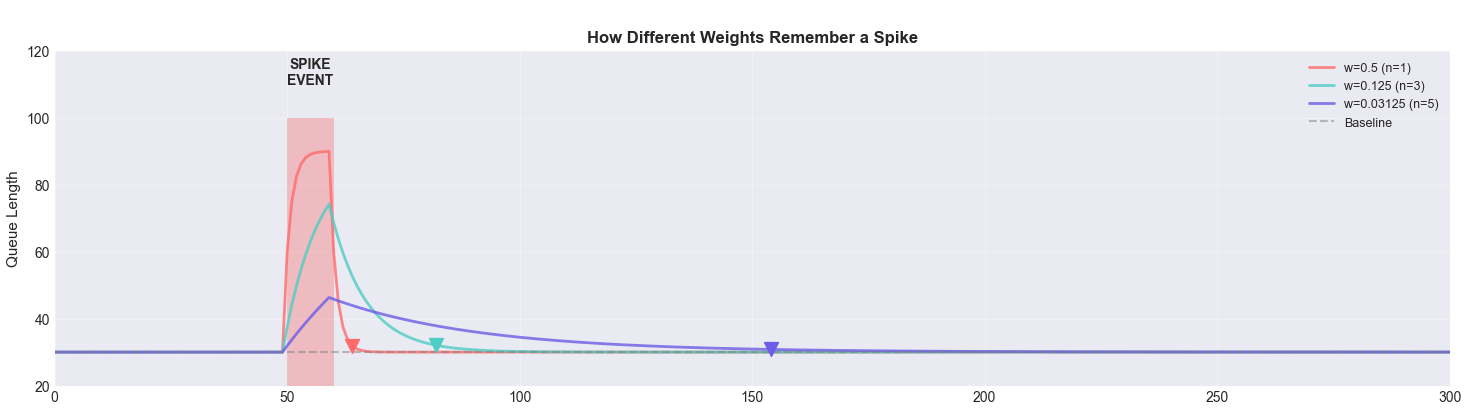
The Half-Life Perspective

So far we’ve started with $w$ and explored its effects. But in practice, you often know the behavior you want and need to find the right $w$. This is where the half-life perspective becomes invaluable.

Consider radioactive decay—we describe uranium by its half-life (4.5 billion years) rather than its decay constant because half-life is intuitive: “How long until half of it’s gone?” The same approach works for EWMA: “How many samples until the effect of a change is cut in half?”

Say your queue jumps from 100 to 200 packets. That’s a 100-packet step change. The half-life $H$ tells you how many samples it takes for EWMA to close half the gap—to reach 150 packets.

The mathematics connecting half-life $H$ (in samples) to weight $w$:

Given w, find half-life:

Given desired half-life, find w:

Let’s see this in action with that 100 $\to$ 200 packet jump:

• H = 1 sample $\to$ w = 0.5 After 1 sample: EWMA = 150 packets (halfway there in one step!) After 2 samples: EWMA = 175 packets

• H = 8 samples $\to$ w = 0.083
  After 1 sample: EWMA = 108 packets (slow start) After 8 samples: EWMA = 150 packets (halfway there as promised)

With H=1, we absorb the half the change in one sample, i.e. the system reacts very quickly as it has a higher weight ($w=0.5$) vs. H = 8, which results in a relatively lower weight ($w=0.83$).

The half-life approach is powerful because you can specify behavior in terms of time: “I want microbursts (lasting 10ms) to fade quickly but real congestion (lasting 100ms) to register fully.” Convert those times to samples based on your sampling rate, and you have your half-life specification.

The Rise Time Perspective: How Fast Do We React?

Sometimes you don’t care about half-life; you care about how quickly the system responds to a sustained change. We often use the “10% to 90% rise time” - how many samples does it take for the EWMA to move from 10% to 90% of the way to a new steady state?

The relationship is simple:

So if you set your half-life to 4 samples, it takes about 13 samples to mostly complete a transition. This gives us another way to think about choosing $w$:

1. Decide how quickly you need to detect real changes (your rise time requirement)
2. Divide by 3.17 to get your half-life $H$.
3. Compute $w = 1 - 2^{-1/H}$

For instance, imagine if I know that my legitimate traffic patterns change on 100ms timescales, but microbursts last only 1-10ms. If I sample every millisecond:

• You want a rise time of ~100 samples (100ms).
• So $H = \frac{100}{3.17} \approx 32 \text{ samples}$.
• Therefore $w = 1 - 2^{-1/32} \approx 0.021$

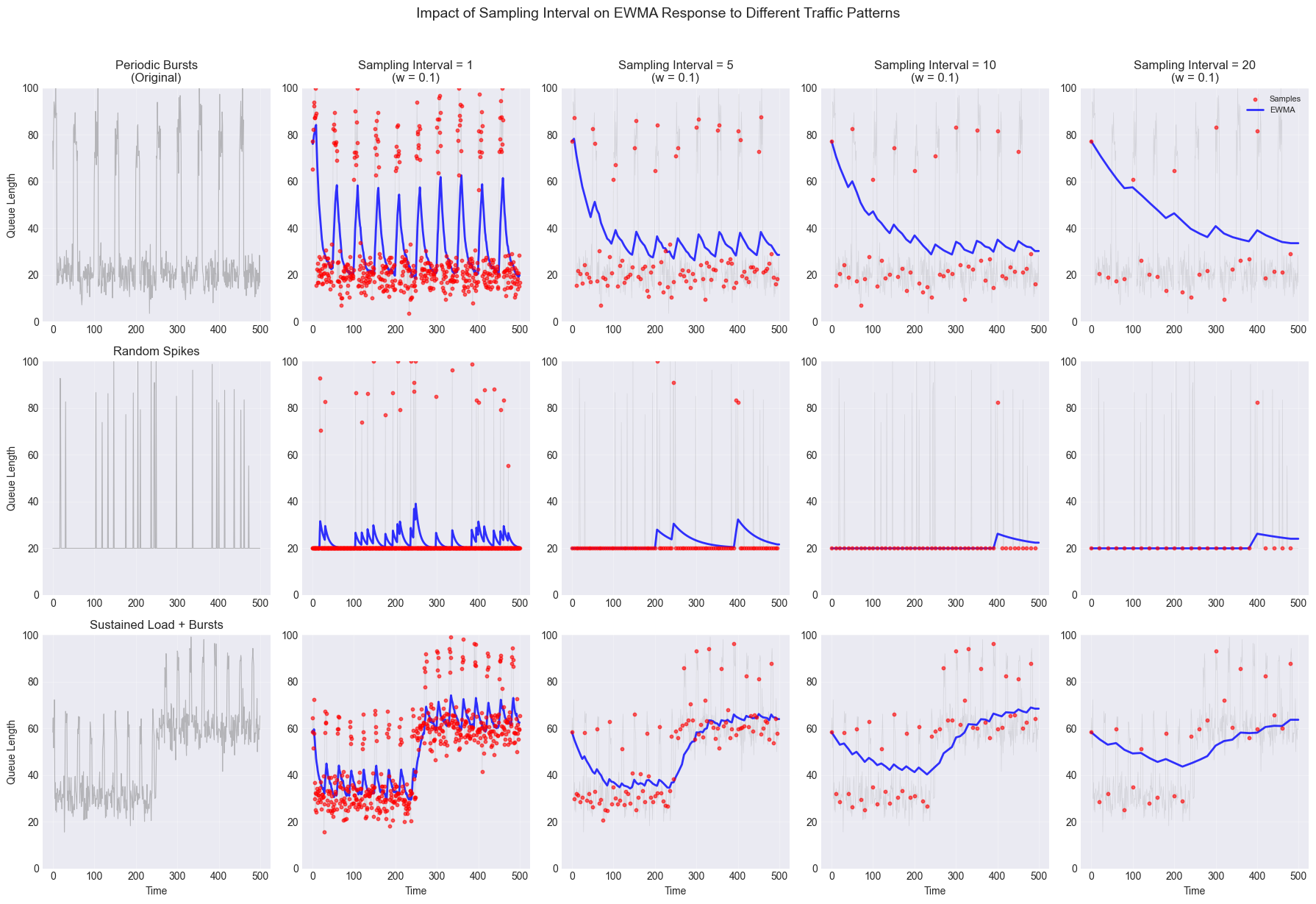
Importance of Sampling Interval ($T_s$)

The sampling interval $T_s$ is the time period between two consecutive measurements. Its duration significantly impacts EWMA accuracy and responsiveness. Shorter sampling interval allows to track short-duration bursts more accurately. The sampling interval must be shorter than the timescale of the changes we are trying to detect.

• With a fixed weight $w$, shorter sampling intervals means the EWMA responds to changes over a shorter absolute time window.
• With a fixed weight $w$, longer sampling intervals means the EWMA has a longer absolute time memory.

Below plot shows for a fixed weight with different sampling intervals.

Sampling Rate Invariance: Keeping Behavior Consistent

EWMA is just a discretized first-order low-pass filter. let’s assume we have tuned our EWMA perfectly with $w = 0.1$, sampling every $10ms$. Now we change our sampling rate to be faster by changing it from 10ms to 1ms. If we keep the same weight $w = 0.1$, our system behavior completely changes! The half-life in real time becomes 10x shorter.

To maintain the same time-based behavior when changing sampling rates, we need to adjust $w$.

Let’s look at an example.

• Sampling period: $\Delta t_{old} = 10ms$
• Weight: $w_{old} = 0.1$
• Time constant: $\tau = -\Delta t_{old}/\ln(1-w_{old}) \approx 95ms$

Now sampling 10x faster ($\Delta t_{new} = 1ms$):

Now we need much smaller $w$. This is because we are updating 10x more often, so each update needs to be gentler to maintain the same overall time constant.

WRED Linear Ramp

So we have this queue with an average Queue depth $Q_{avg}$ (not the instantaneous depth - that will make it too jittery). We want three distinct behaviors:

When the queue is pretty empty ($Q_{avg} \lt Q_{min}$), life is good. When the queue is getting concerning but not critical ($Q_{min} \le Q_{avg} \lt Q_{max}$), we start getting selective. We begin randomly dropping or marking packets with increasing probability as the queue fills up. When the queue is critically full ($Q_{avg} \ge Q_{max}$), we drop or mark every packets that arrive.

Now in the middle zone ($Q_{min} \le Q_{avg} \lt Q_{max}$), we need to decide our drop/mark probability. The simplest thing that could work is a linear ramp:

The fraction $\frac{Q_{\text{avg}}-Q_{\min}}{Q_{\max}-Q_{\min}}$ is just asking “what percentage of the way are we from $Q_{min}$ to $Q_{max}$?”. If $Q_{avg}=Q_{min}$, this fraction =0. if $Q_{avg}=Q_{max}$, this fraction =1, and it scales linearly in between. We then multiply it by $P_{max}$ to get our actual drop probability.

For instance, let’s assume $Q_{min}=20 \text{ packets}$, $Q_{max}=60 \text{ packets}$, and $P_{max}=0.8$. If our average queue is at 40 packets, then:

So we would drop or mark 40% of packets.

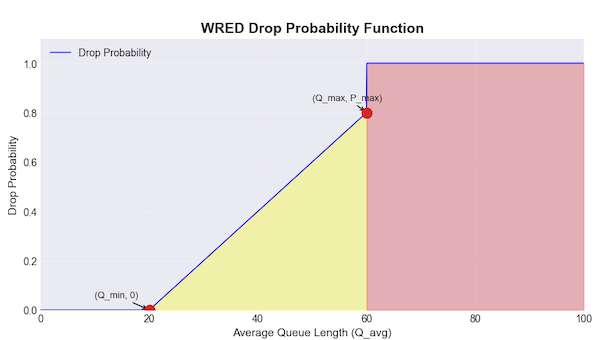
Note: In case of DCTCP, Q_min and Q_max is set to same value, so there is no linear ramp.

RED’s “uniformization” using a packet counter

Naively, we could just flip a biased coin with probability $P_a$ on each packet (where $P_a$ is the linear ramp above). But in practice two things will bite us:

1. Burst clustering. If $Q_{\text{avg}}$ rises quickly, repeated independent trials with the same $P_a$ can produce multiple drops in a tight clump, punishing whichever flow is unlucky.
2. Fairness vs. burstiness. You want drops spaced out so no single flow gets hammered by a few consecutive losses purely due to timing.

There is a two part solution to the above problem. First we know that not all packets are equal in size, and second it uses a packet counter trick to break the natural clustering of random drops.

Let’s start with packet size fairness. Imagine we have 1500 byte packets and 64 byte ACK packets. If we treat them equally for dropping purposes, we are being unfair in terms of Queue consumption. The big packet is taking up 23 times more space compared to the small packet. So we solve this by adjusting the base probability for packet size:

For instance, if our $P_a$ is 0.1 and MaxPacketSize is 1500 bytes, then when 1500-byte packet arrives, its adjusted probability stays at 0.1. But when a 150 byte packet arrives, its probability becomes 0.01:

This is proportional fairness. Now with this size adjusted $P_a$, RED implements the uniformization through packet counting. Instead of each packet having an independent drop probability (which creates clustering), RED keeps track of how many packets have passed since the last drop (the count variable) and computes:

This is creating a “memory” in the system. Each packet that passes increases the count, which makes the denominator $(1-\text{count }\times P_a)$ smaller, which makes $P_a$ larger. This results in creating increasing “pressure” to drop.

Dynamic ECN

The Core Problem: Why Queue Length Lies to Us

Traditional ECN assumes queue length indicates congestion. This made sense when queues had dedicated buffers—30KB queue meant 30KB consumed. But modern switches share a common buffer pool among all queues, breaking this assumption.

With shared buffers, queues borrow space dynamically. Queue A grabs extra during bursts, Queue B releases unused allocation back to the pool. Great for efficiency, but now queue length tells you nothing about actual congestion.

Consider a switch with 100KB shared buffer and two queues:

False positive: Queue A uses 30KB, Queue B uses 5KB. Static ECN marks Queue A for exceeding its 25KB threshold—even though 65KB sits free. You’re signaling congestion at 35% utilization.

False negative: Twenty queues each using 4KB. Static ECN marks nothing—every queue looks fine at 4KB. Meanwhile, you’re at 80% utilization and about to drop packets everywhere.

Same queue length, opposite realities. In shared buffer systems, 30KB might mean plenty of headroom or 4KB might mean imminent collapse—the queue length alone reveals nothing.

D-ECN tracks what actually matters: not “how long is my queue?” but “how much of my current allocation am I using?” Your allocation shifts with pool pressure, and D-ECN’s thresholds shift with it.

How D-ECN’s Dynamic Thresholds Work

Think of D-ECN as replacing a static speed limit sign with a dynamic one that adjusts based on road conditions. Static ECN is like having a fixed “Start braking at 60 mph” rule. D-ECN is like having a sign that says “Start braking when you’re 100 feet from the car in front of you” where that car’s position changes with traffic.

The key insight is that D-ECN tracks a moving target. Your queue’s share of the pool expands and contracts based on how many other queues are active and how aggressively they’re consuming buffer. The mathematics are handled by the buffer manager using alpha parameters, but conceptually it’s simple: when the pool is empty, you might be allowed 100KB. When the pool is under pressure, your allowance might shrink to 20KB.

The threshold for marking moves with this allowance:

This is different from static ECN’s approach:

At its heart, D-ECN computes a threshold using three inputs, but only two are under your control.

D-ECN is implementing three simple rules:

1. Normal case: Mark when you’re within offset bytes of your limit
2. Protection case: Never mark below the floor (prevent over-aggressive marking)
3. Saturation case: Never mark above your actual shared_limit (obviously)

So let’s imagine we have

• DECN_OFFSET = 20KB (your safety margin)
• DECN_FLOOR = 10KB (minimum queue before considering marking)

Scenario 1: Plenty of buffer available Your queue’s shared_limit is currently 100KB.

Threshold = min(100KB, max(100KB - 20KB, 10KB))
         = min(100KB, max(80KB, 10KB))
         = min(100KB, 80KB)
         = 80KB

You’ll mark packets when your queue reaches 80KB, giving you 20KB of headroom.

Scenario 2: Buffer pool getting tight Other queues are now active, your shared_limit shrinks to 25KB.

Threshold = min(25KB, max(25KB - 20KB, 10KB))
         = min(25KB, max(5KB, 10KB))
         = min(25KB, 10KB)
         = 10KB

The floor kicks in! You mark at 10KB instead of 5KB, preventing starvation.

Scenario 3: Extreme congestion The pool is nearly exhausted, your shared_limit is only 8KB.

Threshold = min(8KB, max(8KB - 20KB, 10KB))
         = min(8KB, max(-12KB, 10KB))
         = min(8KB, 10KB)
         = 8KB

Your actual limit becomes the cap. You can’t mark packets for using buffer you don’t have.

This three-case structure elegantly handles the full spectrum from empty to congested without any special cases or mode switches.

The Parameters: What You Actually Control

You only set two parameters for D-ECN, but choosing them correctly is crucial. Let me show you how to think about each one.

DECN_OFFSET: Your Reaction Distance

The offset is fundamentally about time. It’s answering: “How much buffer do I need between when I mark a packet and when the sender reacts?”

This buffer needs to accommodate:

1. Packets in flight that will arrive before the sender even receives the congestion signal
2. Burst absorption for natural traffic variations
3. Safety margin for measurement and reaction delays

Here’s how to calculate it. Start with fundamental parameters:

Where $n$ can be a multiple if we think it takes more than one RTT for the reaction time. For a concrete example with a 10 Gbps link, 100 microsecond RTT, and typical 10-packet bursts:

DECN_FLOOR: Your Minimum Operating Point

The floor prevents pathological behavior when buffers are nearly empty. Without it, you could end up marking packets in a 1KB queue just because the math says your threshold should be negative. The floor should be large enough to:

1. Maintain stable operation for at least one RTT
2. Avoid marking during normal, low-latency operation
3. Provide enough data for accurate congestion detection

A good starting point is:

Where Min_BDP is the bandwidth-delay product of your shortest RTT flows. For a data center with 10 microsecond minimum RTT:

D-ECN is complementary to static ECN—both coexist and operate independently. When either WRED’s probabilistic algorithm or D-ECN’s dynamic threshold triggers, the packet gets marked, providing comprehensive congestion coverage without requiring any changes to your existing WRED configuration.

Packet Trimming Mechanisms in AQM

The Core Idea

Packet trimming is an Active Queue Management (AQM) strategy in which a switch, when experiencing congestion, removes part of the packet—typically the payload—rather than dropping the entire packet. By forwarding a truncated packet that contains only the header and minimal data, the network becomes “lossy” for the payload while still preserving important metadata. This approach maintains crucial information, such as sequence numbers, and provides immediate congestion signals to endpoints without the need to wait for timeouts.

The idea was first proposed as cut payload (CP) and later refined in protocols like NDP. Trimming enables switches to run shallow queues since even when the queue overflows, most packets aren’t entirely dropped. This drastically reduces buffering delay while avoiding throughput collapse: senders quickly learn of congestion and can retransmit lost payloads with minimal delay.

Whenever an egress queue is full, the switch trims off the entire payload and forwards only the packet header. The trimmed header (marked with a “trim” bit) reaches the receiver or possibly is returned to the sender as a congestion signal. By only dropping payload, we avoid conventional packet loss; the receiver still sees a packet header and can immediately infer that the corresponding data segment was lost, prompting a fast retransmit (essentially an early negative acknowledgment). There is a priority header queue so that trimmed headers leapfrog full packets, ensuring the congestion signals propagate quickly. This mechanism prevents livelock: even under heavy incast, header-only packets get delivered promptly, giving senders timely feedback. Full-payload trimming, works well in datacenters with minimal propagation delay – the dropped payload can be retransmitted almost immediately, often arriving before the queue drains.

There is also selective chunk-level trimming scheme which was proposed as part of WAN/Video use cases and QUCO (Quality-aware Cutoff) is one such algorithm.

Preventing Header-Only Livelock

A potential pitfall in trimming is that if too many packets are trimmed, the network could become livelocked sending mostly headers and very little payload. NDP avoids this by using a separate priority queue for trimmed headers. All trimmed packets enter a high-priority queue, ensuring they swiftly reach the receiver, while bandwidth is still allocated to full data packets (to avoid starvation of payload). In an ideal implementation, a WRR/WFQ by byte size can be used. This way, headers (very small) effectively jump ahead, but large packets still get service, preventing a scenario where the switch transmits nothing but headers. If even the header queue becomes saturated (e.g. in extreme incast with thousands of flows), NDP falls back to sending headers back to the source (source-directed congestion notification, Return-to-Sender, Back-to-Sender). An evolution of this idea is Source Flow Control (SFC), which proactively returns trimmed headers to senders once a queue crosses a watermark. SFC (under standardization at IEEE) ensures that when a switch can’t even forward headers to the receiver, the congestion signal is delivered by bouncing the header back to the transmitter. These mechanisms guarantee that some form of congestion feedback (header to receiver or source) always gets through, maintaining stability.

Hardware Implementations

Implementing packet trimming on real switches poses challenges, because most ASICs were not originally designed for dynamic packet resizing on the fly. Several approaches and hardware primitives are used to support trimming.

Mirror-on-Drop (MoD) and Recirculation

Many switch ASICs provide a “mirror on drop” or deflect-on-drop feature in the traffic manager. Normally used for diagnostics (to capture packets that would be dropped), this feature can be repurposed for trimming. When an egress queue is about to overflow, instead of dropping a packet, the traffic manager redirects it to a special recirculation port. Many switch asics allows the traffic manager to directly mirror just the packet header into a MoD queue, without carrying the full payload through recirculation. In those ASICs, the hardware can automatically truncate the packet to a small size when deflecting, which is more efficient. The truncated copy is then enqueued either to the original output port’s header queue (for forward delivery) or to a return-to-sender queue (for SFC) - if ASICs supports it. This design minimizes extra latency – although recirculated headers incur a slight delay and use internal bandwidth, they remain much smaller than full packets. One limitation is oversubscription: if too many packets are deflected at once, the recirculation port per pipeline can become a bottleneck.

Ingress Pipeline Trimming

A better approach is to perform trimming earlier, in the ingress stage, before packets enter the queue. If the ingress pipeline can query the current queue length (or an occupancy threshold flag) for the egress port, it could decide to trim packets preemptively on arrival. Implementing ingress trimming is complicated if precise queue information isn’t available or if there are many pipeline stages of latency in reading the queue state. Design must account for in-flight packets already in the pipeline which might overflow the queue before the trim logic activates.

Conclusion

We started with the classics—RED and its per-class variant WRED—which were the first practical ways to “tap the brakes” before a queue hit tail-drop. By marking/dropping probabilistically as a smoothed queue crosses a minimum→maximum band, they keep delay bounded and prevent herd backoff, especially when paired with ECN. The main goal remains the same: to detect congestion early enough for senders to respond before buffer capacities are exceeded, all while not penalizing short bursts of traffic.

The challenging aspect lies in the implementation—specifically, selecting Exponentially Weighted Moving Average (EWMA) weights and sampling methods that align with the time scales of the traffic. Additionally, it involves setting moving thresholds with parameters (like DECN_OFFSET and DECN_FLOOR) that correspond effectively to the Bandwidth-Delay Product (BDP), burst size, and desired reaction time. We also examined how Packet Trimming can help reduce reaction time.

Once properly calibrated, AQM can replace the volatility caused by tail drop with a more controlled and fair signaling approach. This helps maintain short queues, keeps delays bounded, and ensures high utilization of network resources. I hope this was useful.

References

• Dynamic ECN
• Re-architecting datacenter networks and stacks for low latency and high performance
• Implementing packet trimming support in hardware
• Enhancing End-to-End Transport with Packet Trimming
• EWMA
• Exponential Smoothing
• WRED
• Impulse Response
• Half-Life of EWMA
• SFC: Near-Source Congestion Signaling and Flow Control
• Cut Payload